样本均值是统计学中考量一组数据的集中趋势的统计量之一。设x1, x2, ..., xn是总体x中的一个样本，则统计量样本均值的计算方法如下：

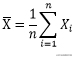
计算样本均值的公式

在r中，mean()函数用于计算样本的均值，其使用格式为：

mean(x, trim=0, na.rm = false, ...)

其中，参数x为计算对象，可以是向量、矩阵、数组或数据框；

trim用于设置计算均值前去掉两端数据的百分比，即计算结尾均值，取值在0~0.5之间；

na.rm为逻辑值，指示是否允许有缺失值(na)的情况，默认为false（不允许）;

...为附加参数。

 

假设某班级20名学生的英语成绩为88,78,67,69,62,100,73,45,70,60,93,97,84,82,81,73,68,76,77,92。计算其均值。

编写r程序如下：

x<-c(88,78,67,69,62,100,73,45,70,60,93,97,84,82,81,73,68,76,77,92)

mean(x)

结果为76.75。如计算结尾，则：

mean(x,trim=0.05)

则结果是:77.22。