前面的文章我们已经介绍过虚数单位i，我们定义i^2=-1。

 

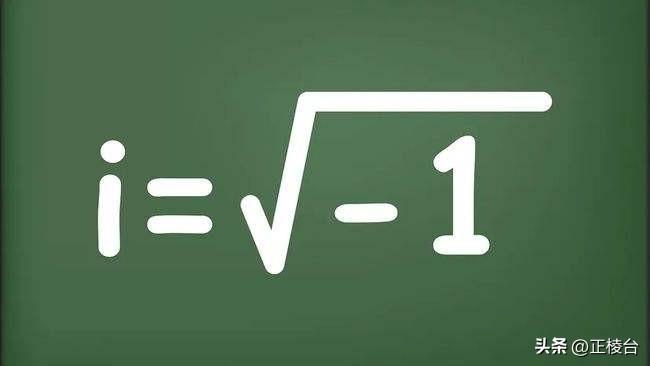
类似地，我们就可以计算：

i^3=i^2×i=-1×i=-i

i^4=i^3×i=-i×i=-i^2=-(-1)=1

i^5=i^4×i=1×i=i

…………

i^5=i^1，i^6=i^2，i^7=i^3，i^8=i^4，……

我们可以看到，i的实数次方其结果有可能是一个实数，也有可能是一个虚数。同时也很容易观察到对于i^n，其周期t=4，我们可以进一步得出一般性结论：

i^(4k n)=i^n，k∈整数集z

对于虚数单位i的实数次方，我们还是比较容易理解的。今天我们来讨论一个有意思的问题，虚数的虚数次方应该怎么计算呢？比如i的i次方：i^i等于多少呢？这个结果是实数还是虚数呢？

i^i=?

要想解决这个问题，我们还是需要借助到强大的欧拉公式：e^(ix)=cos(x) i×sin(x)

 

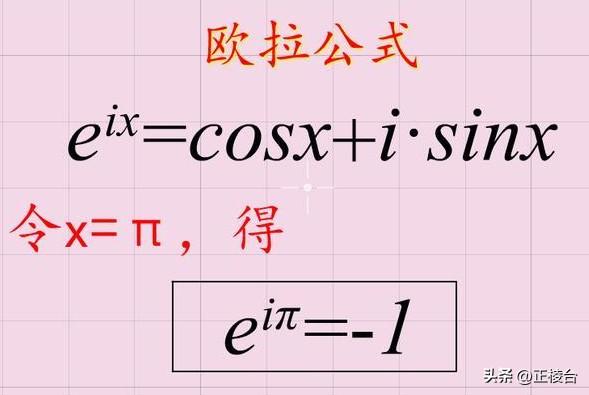
i=0 i=0 i×1

=cos(π/2) i×sin(π/2)=e^[i×(π/2)]

i^i={e^[i×(π/2)]}^i=e^{[i×(π/2)]×i}

=e^[(i^2)×(π/2)]=e^[(-1)×(π/2)]=e^(-π/2)

i^i=e^(-π/2)=1/e^(π/2)=1/√(e^π)

我们可以看到i^i=e^(-π/2)=1/√(e^π)

其结果是一个实数，用计算器算一下：

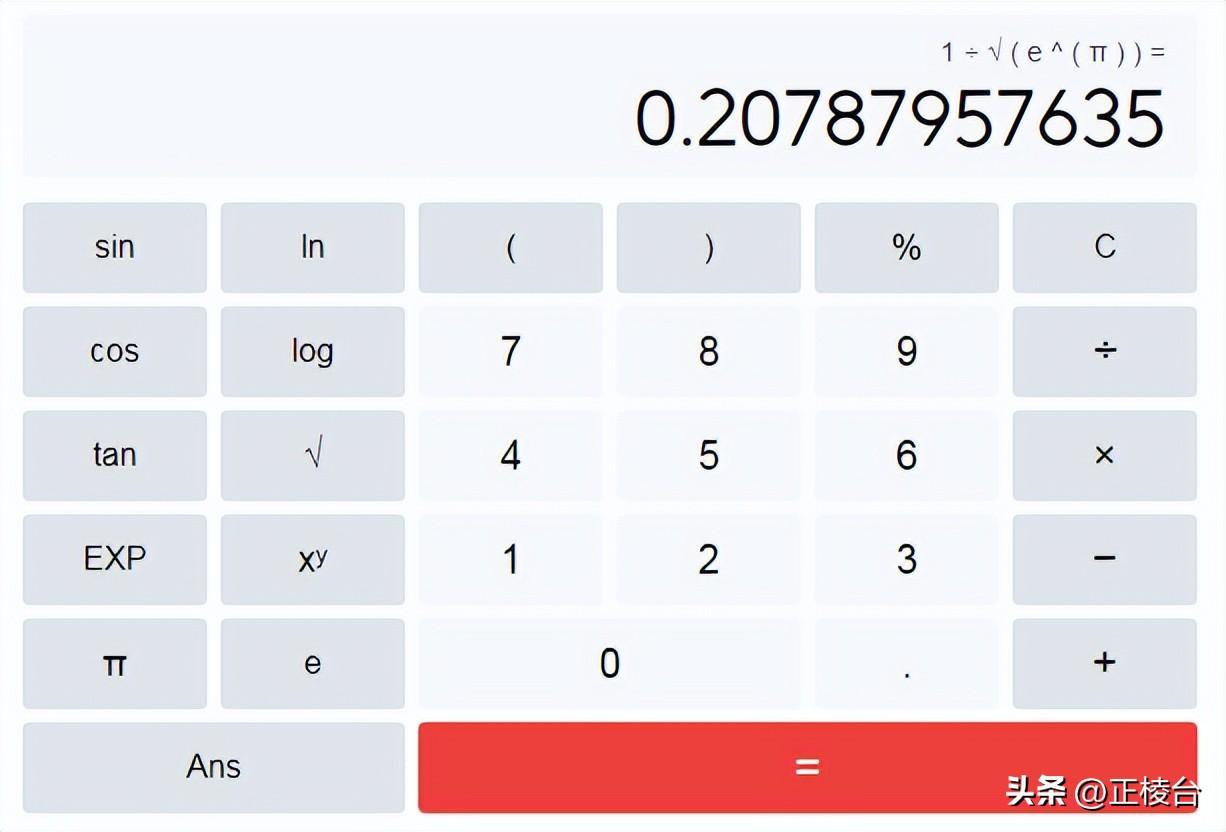
i^i=1/√(e^π)

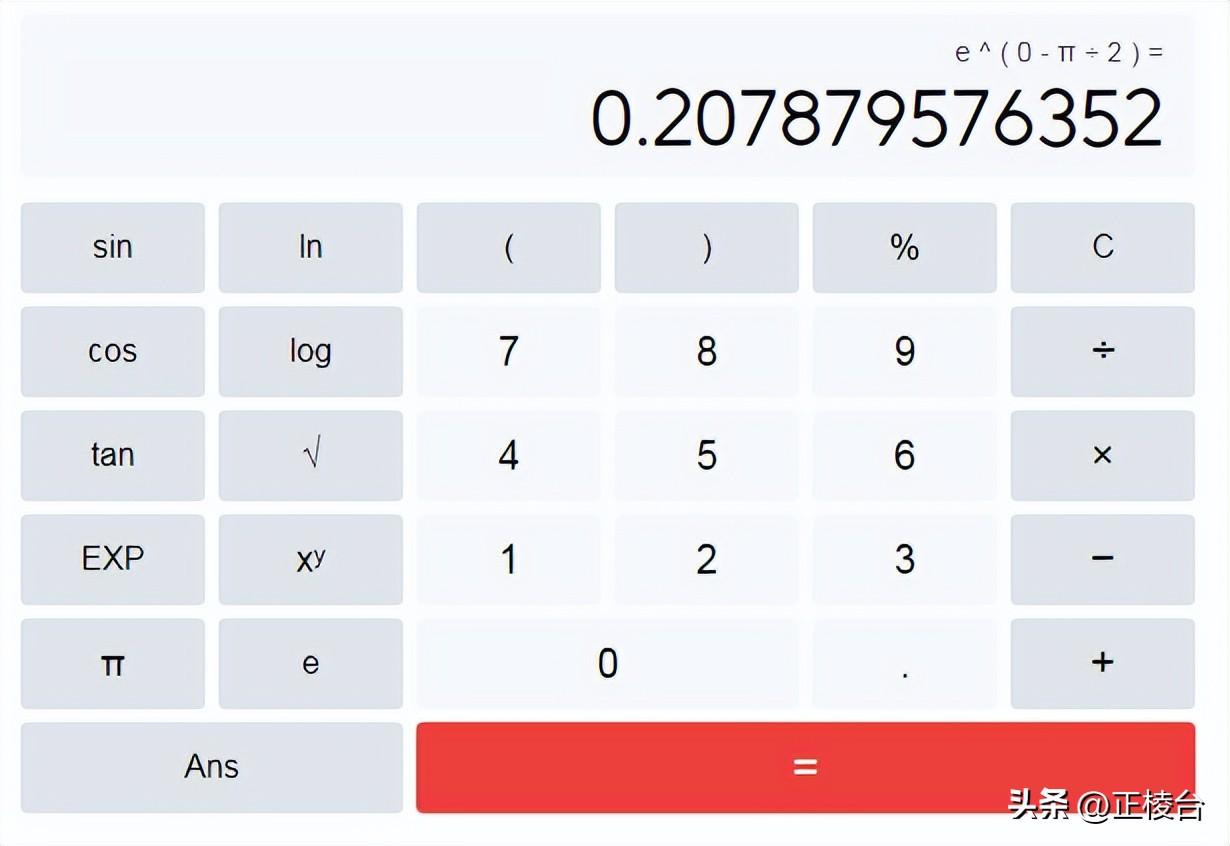
i^i=e^(-π/2)

这个结果确实有些令人难以接受，但这就是事实，i^i=0.207829……

这里需要强调地是，i^i=e^(-π/2)=1/√(e^π)=0.207829……只是i^i其中一个计算结果，我们称之为主值。

e^(ix)=cos(x) i×sin(x)，若0≤x＜2π，则称e^(ix)为计算结果的主值。

所以对于i^i，完整的计算结果如下：

i=0 i=0 i×1

=cos(π/2) i×sin(π/2)=e^[i×(π/2)]

 

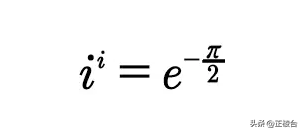
注意到正弦函数y=sin(x)与余弦函数y=cos(x)的最小正周期都是2π

cos(π/2 2kπ)=cos(π/2)=0，k∈z

sin(π/2 2kπ)=sin(π/2)=1，k∈z

i=0 i=0 i×1=cos(π/2 2kπ) i×sin(π/2 2kπ)

=e^[i×(π/2 2kπ)]

i^i={e^[i×(π/2 2kπ)]}^i

=e^[-(π/2 2kπ)]

=1/e^(π/2 2kπ)，k∈z

当k=0时，i^i的主值为：

i^i=e^(-π/2)=1/e^(π/2)=1/√(e^π)

类似地，我们还可以计算i次根号下i，也就是i的(1/i)次方：i^(1/i)

 

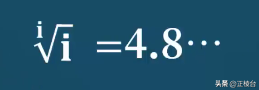
1/i=i/i^2=i/(-1)=-i

i^(1/i)=i^(-i)=1/i^i

前面我们已经计算出，i^i的主值为：

i^i=e^(-π/2)=1/e^(π/2)=1/√(e^π)

所以i^(1/i)的主值为：

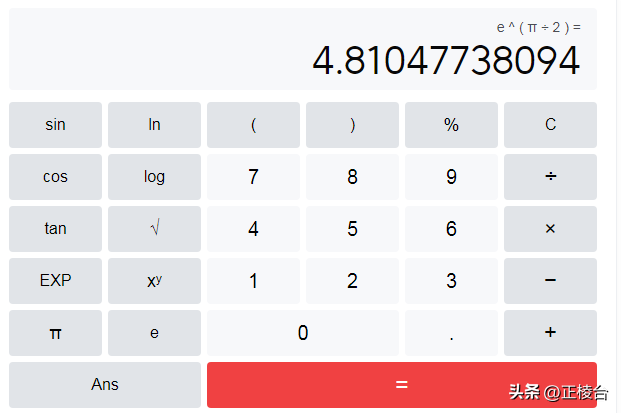
1/e^(-π/2)=e^(π/2)=√(e^π)

其结果仍然是一个实数，再用计算器算一下：

 

最后总结一下，对于计算i^x，首先利用欧拉公式：

i=0 i=0 i×1

=cos(π/2) i×sin(π/2)=e^[i×(π/2)]

i^x={e^[i×(π/2)]}^x=e^[(ix)×(π/2)]

i^x=e^[(ix)×(π/2)]

很显然地是，如果x是纯虚数x=ai，a∈r且a≠0

ix=i×ai=a×i^2=a×(-1)=-a

i^x=e^[(ix)×(π/2)]=e^[(-a)×(π/2)]

也就是说：i的纯虚数次方必然为一个实数。